Teoría del diafragma rodante de DiaCom
La Figura 1 ilustra la reacción de presión en el diafragma. Se puede ver que casi toda la carga de presión es soportada por la cabeza del pistón y solo una pequeña cantidad de la presión del líquido o gas es soportada por la estrecha circunvolución del diafragma. Observe también en la Figura 1 que las líneas de presión unitaria (que actúan en planos horizontales porque deben ser normales a la superficie) fuerzan el diafragma contra el pistón y las paredes laterales del cilindro en la parte del diafragma en contacto con la pared del cilindro y la falda del pistón.
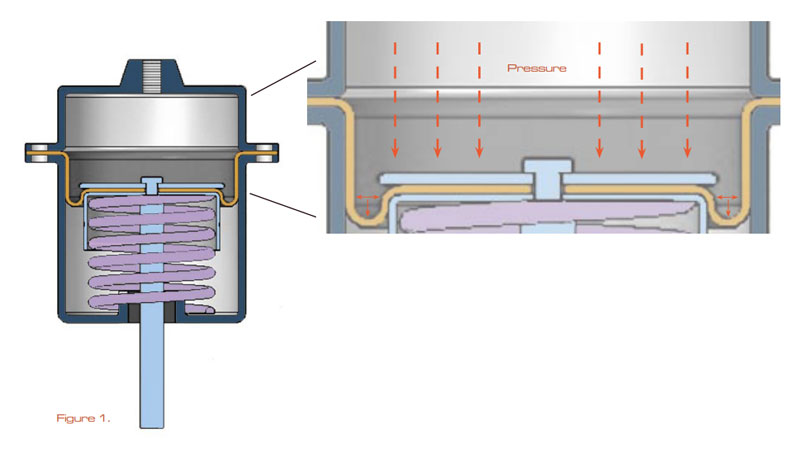
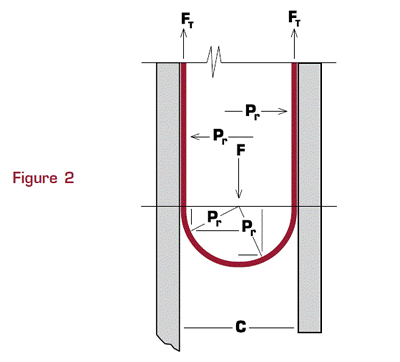
Las líneas de fuerza que actúan sobre la parte del diafragma que no está en contacto con el cilindro o la falda del pistón (el segmento semicircular de la convolución) se muestran en la Figura 2.
Cada línea de presión unitaria (Pr) actúa de forma normal al segmento semicircular; por tanto, cualquiera de las líneas de presión puede reemplazarse por su componente horizontal y vertical. Los componentes horizontales, actuando en oposición, se anulan entre sí.
La suma de los componentes verticales de las presiones unitarias que actúan sobre este segmento semicircular se suma a la fuerza de presión total (F) y es igual a la presión normal en la proyección de este segmento.
Considerando una unidad (1 pulgada) de longitud circunferencial del diafragma, lo anterior es:
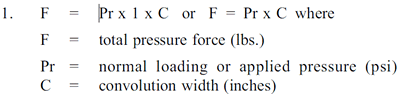
La fuerza total F es soportada igualmente por el refuerzo de tela del diafragma en el pistón y la pared del cilindro (ver Figura 2). Por lo tanto, la fuerza de tensión FT (libras) en cualquiera de las paredes es simplemente la mitad del valor de F o
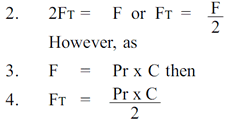
Donde FT es la fuerza de tensión en la pared lateral del diafragma para cada unidad de longitud circunferencial. Dado que la fuerza de tracción FT y la tensión de la tela SF son idénticas, la ecuación 4 se puede expresar en términos de la tensión de la tela:

La tensión de la tela se puede calcular usando la ecuación 5. Por ejemplo, si un diafragma de 3 pulgadas de diámetro con un área de presión efectiva de 6,35 pulgadas cuadradas y un ancho de convolución de 0,156 se somete a una presión de carga de 100 psi, el total resultante de empuje es de 635 libras. Sin embargo, la tensión de la tela en la circunvolución estrecha es solo:
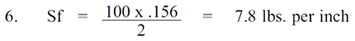
Los materiales de tela están disponibles en resistencias a la tracción superiores a 7,8 libras. por pulgada. Por lo tanto, los anchos de convolución muy estrechos con valores de tensión bajos resultantes en las fibras de la tela permiten que los diafragmas se utilicen en aplicaciones que implican altas presiones de trabajo.
En efecto, los diafragmas rodantes DiaCom son recipientes a presión que tienen un volumen variable y paredes laterales móviles flexibles. Como en cualquier otro recipiente a presión, su resistencia debe considerarse con respecto a los factores de seguridad. Generalmente, los diafragmas se pueden diseñar con un factor de seguridad grande. En efecto, esto significa que la presión máxima de trabajo segura será una fracción de la presión que causaría fallas en el área de convolución. (En algunas aplicaciones de aeronaves donde las presiones de trabajo son tan altas como 1000 psi y los requisitos del ciclo total son bajos, los factores de seguridad aumentan sustancialmente).
El departamento de ingeniería de DiaCom recomendará el análisis de tensión real y la selección de tejidos para cada aplicación.
Solo para consultas e información sobre productos:

